チェバの定理の解説とその証明方法について
メネラウスよりもはるかに覚えやすいチェバの定理について学びます。
チェバの定理の概要
三角形ABCがあり、その各々の頂点から辺に向けて線を引きます。
その線が一点で交わる時に、三角形の頂点と引いた線との交点との比について、
以下のような公式が成り立ちます。
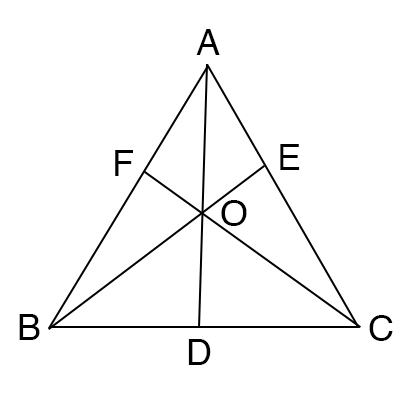
$$\displaystyle \frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1$$
これをチェバの定理といいます。
チェバの定理の覚え方
三角形の頂点 → 線分への交点 → 三角形の頂点・・・
と時計周り・半時計周りに一周すると覚えます。
図で示すとこんな感じです。
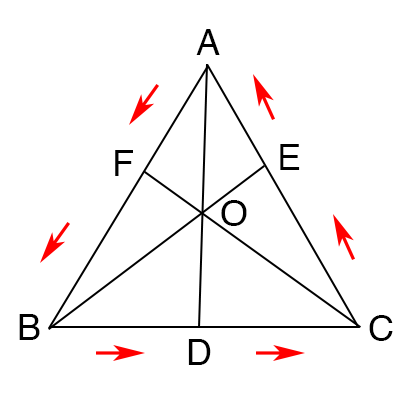
チェバの定理証明
チェバの定理はメネラウスの定理を利用すると、簡単に求めることができます。
メネラウスの定理と証明方法についてはこちらでまとめています。
逆に、素で求めようとすると対比で求めるので、工程が大変。
まず、下図のように三角形ABDと線BDの延長線上の点Cから線ABに引いた直線FCを引き、
メネラウスの定理が利用できるようにします。
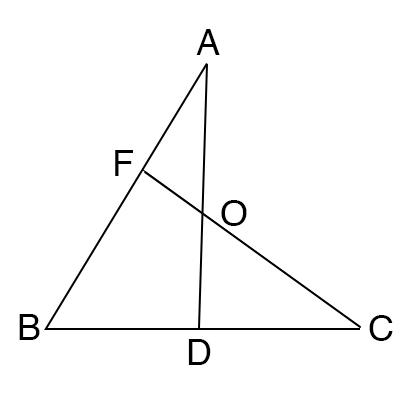
メネラウスの定理より、
$\displaystyle \frac{AF}{FB} \cdot \frac{BC}{CD} \cdot \frac{DO}{OA} = 1 - ①$
次は、下図のように三角形ADCと直線BEに対してメネラウスの定理を用いて、
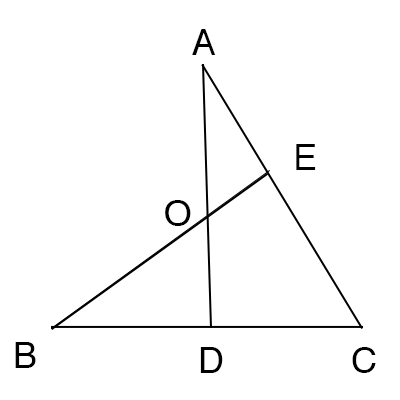
$\displaystyle \frac{DB}{BC} \cdot \frac{CE}{EA} \cdot \frac{AO}{OD} = 1 - ②$
①②の辺々をかけて、
$\displaystyle \frac{AF}{FB} \cdot \frac{DB}{BC} \cdot \frac{CE}{EA} = 1$
となりチェバの定理を簡単に求めることができます。
初版:2019/2/1
改定:2023/2/6(ODと書くところをOP間違って書いていたところを修正)