三角形の内心とは
三角形の内心について解説します。
三角形の内心の定義
三角形の3つの内角の2等分線の交点のことを三角形の内心といいます。
図にすると以下のようになります。
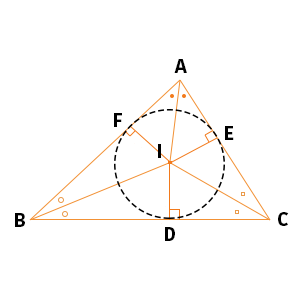
三角形の内心の性質
上図のように三角形の内心をIとして、Iから直線AB・ACに引いた垂線をそれぞれ、IF,IEとします。
直角三角形AFIとAEIに着目すると、直角三角形の合同条件のひとつ斜辺と一つの角が等しいことから、
直角三角形AFIとAEIは合同であり、IF = IEであることがわかります。
直線BCに引いた垂線Dに関しても同様に考えると、
IF = IE = ID
となるので、内心Iは三角形ABCの内接円の中心となることがわかります。
つまりは、
IA = IB = IC = 半径
となります。
初版:2018/10/31 改定:2021/6/15