正弦定理を図で証明する

三角関数の項目で学ぶ、正弦定理の証明を図を使っておこないたいと思います。
まずは、正弦定理とはなんぞやというところから

三角形ABCの外接円の半径をRとします。
すると、以下の公式が成り立ちます。

$${a \over sinA} = {b \over sinB} = {c \over sinC} = 2R$$

次にこれを証明します。

正弦定理を証明するために、対象の角度を場合分けして考えます。
まずは、対象の角度をAとした時に$A = 90°$とした場合について考え、
以下に図示します。

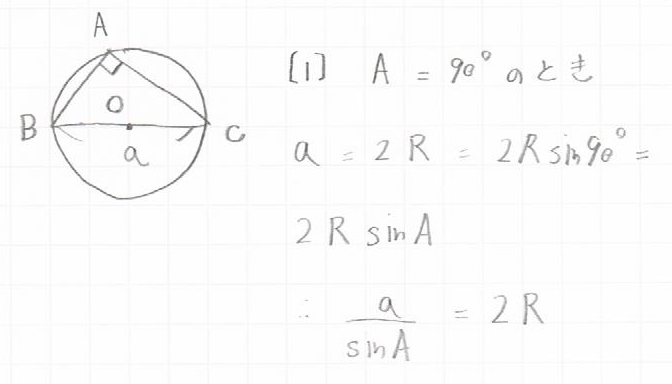
$A$が$90°$の時、直線$a$は円の中心点$O$を通り直径になるので、$a = 2R$となります。
また、$sin90°$は$1$なので、以下のように変換することができます。

$a = 2R = 2Rsin90° = 2RsinA$

となり、

$\displaystyle {a \over sinA} = 2R$
となります。

つづいて、鋭角の場合です。
以下の図を例とします。

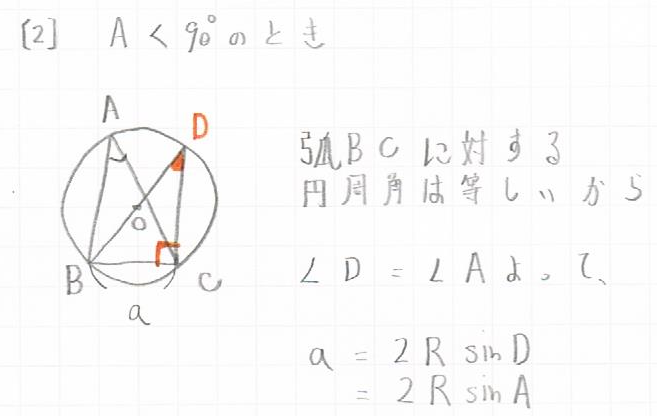
弧$BC$に対して、頂点$D$を設け、$BD$が中心点$O$を通るようにすると、
$\angle D$に対して、角度が$90°$の場合の正弦定理を使うことができます。

弧BCに対する円周角は等しいので、
$\angle D = \angle A$

よって

$a = 2RsinD = 2RsinA$

となります。

最後に鈍角の場合の証明です。
以下の図を例とします。

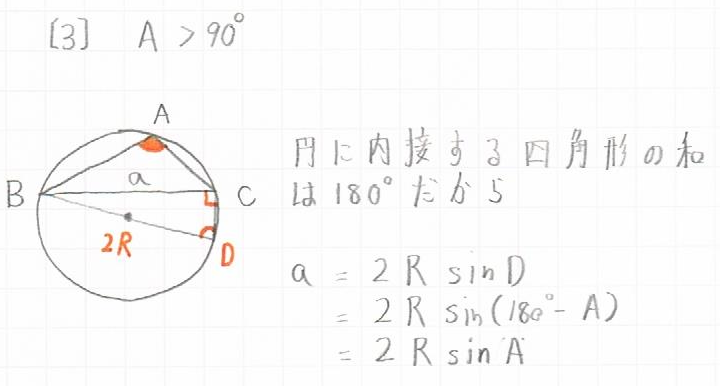
まず、$BD$が円の中心点を通るように、点$D$をおきます。
円に内接する四角形の対角の和が$180°$であることを利用して、

$a = 2RsinD$
$a = 2Rsin(180° - A)$
$a = 2RsinA$

角$A$が鋭角、90°、鈍角いずれの場合も三角形の他の角B、Cは鋭角、90°,鈍角のパターンが当てはめられるので、
角B、Cについても$\dfrac{b}{sinB}, \dfrac{c}{SinC}$が当てはまることがわかります。

正弦定理は図示すると、簡単に求めることができるんですね。

初版:2018/6/5
初版:2023/5/1(解説を追加しました)

Tweet