メネラウスの定理の解説とその証明方法について
非常に覚えにくい、メネラウスの定理について、忘れないようにまとめたいと思います。
メネラウスの定理の概要
三角形ABCがあり任意の直線lが三角形の3辺AB,BC,CA(または辺の延長線上)の交点をF,D,Eとします。
すると、その時次の等式が成立します。
$\displaystyle \frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1$
この関係を図解すると、下図のようなイメージになります。
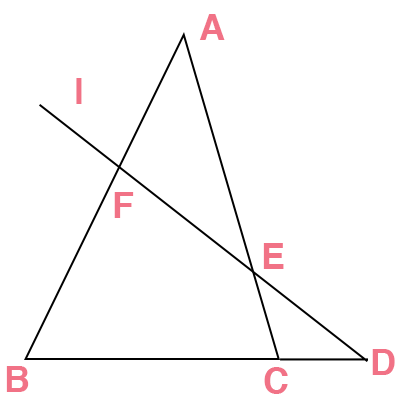
メネラウスの定理の覚え方
メネラウスの定理の公式は、非常に覚えにくいと思いますが、
ルールに沿って考えると覚えやすくなります。
それは、三角形の頂点から、直線lの交点へ行き、その交点から、三角形の次の頂点に向かうというルールです。
これを図で示すと以下のようになります。
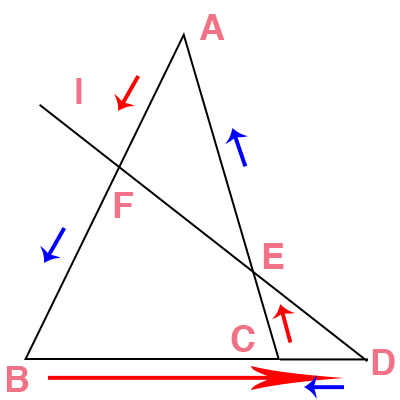
赤の矢印が、三角形の頂点から三角形の辺と直線の交点に向いており、
青の矢印が、直線の交点から三角形の頂点へと向いています。
メネラウスの定理はこれを繰り返すことで、導くことができます。
メネラウスの定理の証明方法
メネラウスの定理は、
平行線を引いて相似の三角形を作り出し、その辺の比を利用して証明することができます。
では、メネラウスの定理を図解しながら証明します。
下図のように、線ABと並行な線を点Cから引いて、線分Lとの交点をKとします。
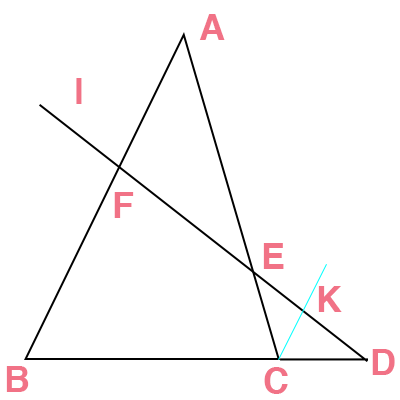
続いて、三角形FBDと三角形KCDが相似であることから、
$BD:CD = BF:CK$
$BD \cdot CK = CD \cdot BF$
ここで、$CD \cdot CK$で両辺を割って
$\displaystyle \frac{BD}{CD} = \frac{BF}{CK} - ①$
続いて、三角形EAFと三角形ECKが相似であることから、
$AE:EC = AF:CK$
$AE \cdot CK = EC \cdot AF$
両辺を$EC \cdot CK$で割って
$\displaystyle \frac{AE}{EC} = \frac{AF}{CK} - ②$
①より、$\displaystyle CK = \frac{BF \cdot DC}{BD}$
CKを②に代入して
$\displaystyle \frac{AE}{EC} = \frac{AF}{\dfrac{BF \cdot DC}{BD}}$
$\displaystyle \frac{AE}{EC} = AF ÷ \frac{BF \cdot DC}{BD}$
よって、
$\displaystyle \frac{AE}{EC} = \dfrac{AF \cdot BD}{BF \cdot DC}$
ここで、$\displaystyle \frac{EC}{AE}$を両辺にかけることによって、メネラウスの定理を導くことができます。
$\displaystyle \frac{EC}{AE} \cdot \frac{AE}{EC} = \frac{AF \cdot BD \cdot EC}{BF \cdot DC \cdot AE}$
整理して、
$\displaystyle 1 = \frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA}$
以上、メネラウスの定理は補助線を引いて、三角形の相似を利用することで求められました。
初版:2019/1/28
更新:2023/2/7(わかりやすいように文言の変更などをしました)