2直線のなす角を$tan$を使って求める方法

2直線のなす角を$tan$を使って求める前に、$tan$の性質について考えてみます。

まずは、このことについて考えてみます。

以下の図のように、
直線$y = mx + n$と
$y = mx$があるとします。

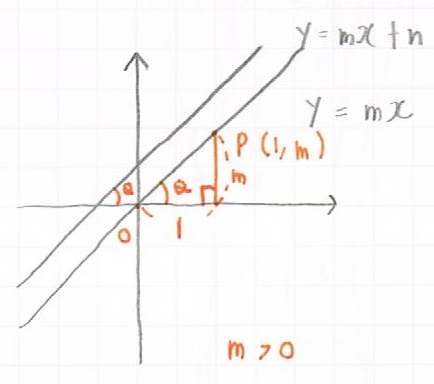
$y = mx$に関して、
$x = 1$の時、直線上の点は$P(1,m)$となります。
ここで、直角三角形$POx$について

$tanθ = m$となり、傾き$m$が$tanθ$と同意であることがわかります。
$n$が0でない場合も同様です。 $m < 0$の場合は下図のようになります。

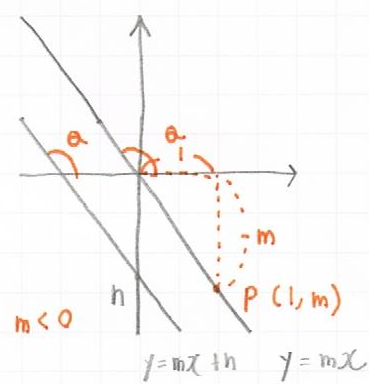
これを踏まえて2直線のなす角についての問題を解いてみます。

まず、直線①と②を$y=$の形に変形します。

$y = -{\sqrt3}x + 3$

$y = x + 2$

この2直線を図示すると、以下のようになり。
2直線の鋭角であるなす角をθとします。

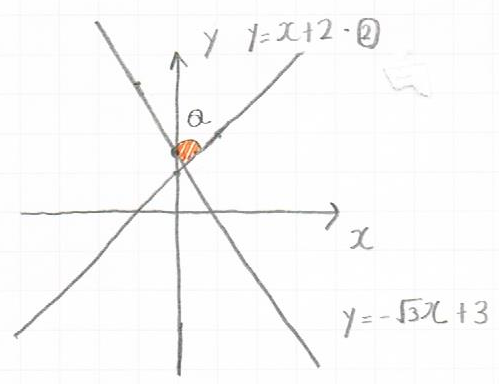
これを、先の$tan$と直線の傾きの図に照らし合わせるために、切片を0とした直線に置き換えます。

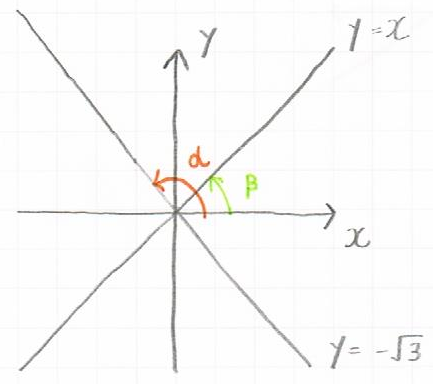
直線①、②の$y > 0$部分と$x$軸のなす角を、$α(0° < α < 180°),β(0° < β < 180°)$とすると、

①の傾きが$-{\sqrt3}$だから
$tanα = -{\sqrt3}$

$α = 120°$

①の傾きが1だから
$tanβ = 1$

$β = 45°$

図より
$θ = α - b = 120° - 45° = 75°$

このように$tanθ$と直線の傾きを結びつけることで、簡単に求められます。

初版:2018/5/31

Tweet