2次関数の放物線と直線の共有点の個数の問題の解法

2次関数の放物線と直線の共有点の個数の問題の解法をまとめます。
まずは、例題から。

共有点の個数を求めるので、$y$を入れ替えて、判別式にて、解の個数を出せばokです。

$y$を消去して、

$-x^2 = -2x + k$
$x^2 -2x + k = 0 ・・ ①$

①について、判別式より
$\dfrac{D}{4} = (-1)^2 - k = 1 - k$

$k < 1$のとき $D > 0$
①は異なる2つの解をもち、共有点は2個

$k = 1$のとき $D = 0$
①は重解をもち、共有点は接点で1個

$k > 1$のとき $D < 0$
①は解をもたず、共有点は0個

よって、
$k < 1$のとき2個、$k = 1$のとき1個(接点),$k > 1$のとき0個

ここで、係数$k$を分離するときの解法も見て見ましょう

$-x^2 = -2x + kを-x^2 + 2x = k$

と置いて、
放物線$y = -x^2 + 2x$と
直線$y = k$との共有点と考えて、個数を求める方法があります。

以下の図のようなグラフに置き換えることができます。

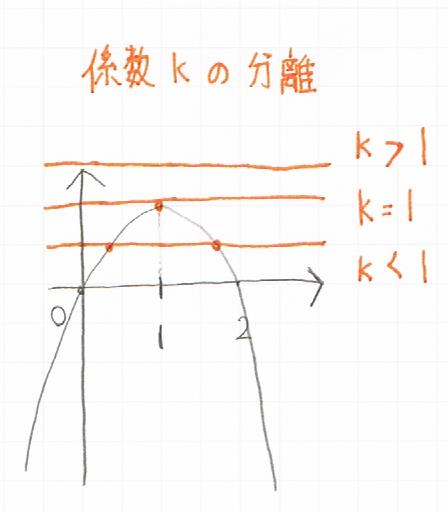
図で表すと明確に理解できます。

初版:2018/5/21