2次不等式の成立条件の解法テクニック

2次不等式の成立条件の解法テクニックに関してまとめます。
では、例題を。

一方だけが実数解をもつということで、範囲に気をつける必要があります。
そして、実数解をもつということで、解の公式の判別式を利用します。
a = 0の場合の場合分けにも気をつける必要があります。
では、解答例を

$ax^2 -3x + a = 0$ ・・・ ①について

$a != 0$のとき、
$D1 = (-3)^2 -4 a \cdot a = 9 - 4a^2$

$a = 0$のとき $-3x = 0$($a = 0$の時解をもつということ)

$x^2 - ax + a-2 - 3a = 0$ ・・・ ②について

$D2 = (-a)^2 -4(a^2 -3a) = 3a(4 - a)$

①が解を持つ条件は、$- \dfrac{3}{2} <= a <= \dfrac{3}{2}$ ・・・ ③

②が解を持つ条件は、$0 <= a <= 4$ ・・・ ④

片方だけが実数解をもつので、③・④が共通解を持たないように注意します。
範囲は下図のようになります。

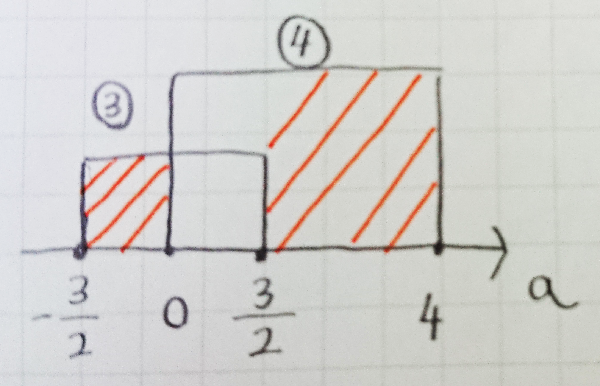
③・④の一方だけが成り立つaの範囲だから

$- \dfrac{3}{2} <= a < 0,\dfrac{3}{2} < a <= 4$

初版:2018/5/14
更新:2023/4/17(整列しました)

Tweet