角の2等分線の公式を図で証明する

角の2等分線の公式を図を使って証明します。
まず、角の2等分線の公式とは以下のようなものです。

三角形ABCにおいて、点Aから2等分線をBCに向かって引き、
その交点をDとすると

$$BD : CD = AB : AC$$

となります。

この証明を正弦定理を使って行いたいと思います。
まず、以下のような図を書きます。

頂点Aから辺BCにむけて、角Aの2等分線を引き、
$\angle ADB = α$とします。

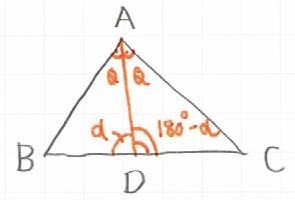
三角形ABDで正弦定理により

$\displaystyle {BD \over sinθ} = {AB \over sinα} --- ①$

三角形ADCで正弦定理により

$\displaystyle {AC \over sin(180° - θ)} = {CD \over sinθ} --- ②$

①よりsinθを両辺にかけて

$\displaystyle BD = {sinθ \over sinα}AB$ --- ③

$\displaystyle sin(180° - α) = sinα$ を②に用い、両辺にsinθを掛けて

$\displaystyle CD = {sinθ \over sinα}AC$ --- ④

③④の比が一緒だから

$$BD : CD = AB : AC$$

と求めることができます。

初版:2018/6/8

Tweet