三角比の性質のまとめとその証明

試験に出る以下の3つの三角比の代表的な性質をまとめます。

$sin^2θ + cos^2θ = 1$

$tanθ = \dfrac{sinθ}{cosθ}$

$1 + tan^2θ = \dfrac{1}{cos^2θ}$

証明をするのに、下図のような単位円を書きます。

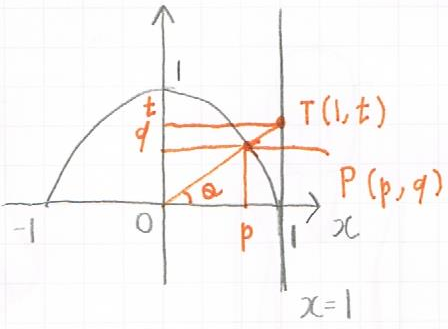
単位円周上に、$\angle POx = θ$となる点$P(p,q)$をとると

$cosθ = p \cdot \cdot ①$
$sinθ = q \cdot \cdot ②$
$tanθ = \dfrac{q}{p} = \dfrac{t}{1} = t,p \ne 0$

図より三平方の定理を使って、
$p^2 + q^2 = 1$
①・②より $sin^2θ + cos^2θ = 1$

③をベースに①・②を代入して
$tanθ = \dfrac{sinθ}{cosθ}$

$sin^2θ + cos^2θ = 1$の両辺を$cos^2θ$で割ると、
$tan^2θ + 1 = \dfrac{1}{cos^2θ}$

となりそれぞれ求めることができます。

初版:2018/5/30

改訂:2023/5/17(分数の表記をみやすくした)

Tweet