トレミーの定理とその証明方法について

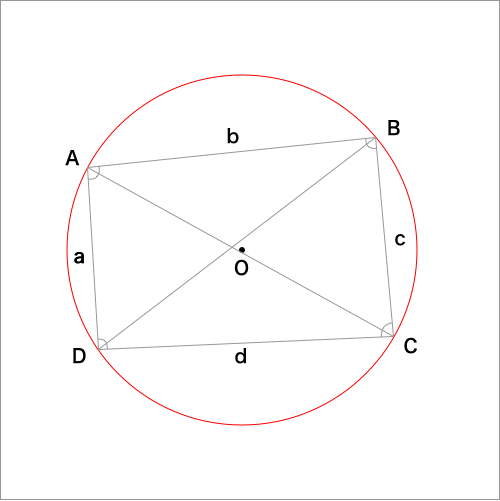
下図のように円に内接する四角形ABCDにおいて

\(AC \cdot BD = AD \cdot BC + AB \cdot DC\)

が成り立つ、これをトレミーの定理という。

下図を参考にします。

余弦定理および内接四角形の性質より、

\(BD^{2} = a^{2} + b^{2} -2ab\cos A\)

\(BD^{2} = c^{2}+d^{2} - 2cd\cos C = c^{2}+d^{2} + 2cd\cos A\)

が成り立つ。ここからcosAを消去して、

\((ab + cd)BD^{2} = (ad + bc)(ac + bd)\) - ①
また、ACについて同様に考えて

\((ad + bc)AC^{2} = (ab + cd)(ac + bd)\) - ②

となるから、① × ②より

\((ab+cd)(bc+ad)AC^{2}\cdot BD^{2}=(ac+bd)^{2}(ad+bc)(ab+cd)\)

この式を整理して

\((AC \cdot BD)^2 = (ac + bd)^2\)

\(AC \cdot BD = ac + bd\)

辺を元に戻すと

\(AC \cdot BD = AD \cdot BC + AB \cdot DC\)

初版:2021/6/24

Tweet