数列シグマ記号の公式と証明方法まとめ

数列の記号シグマの使い方をまとめたいと思います。
$\displaystyle \sum$はプログラムでも様々な場面でよく見る記号なので、理解しておく必要があります。

$\displaystyle \sum$はギリシャ文字で英語のS(Sum合計)に相当します。
つまりは、合計を求める記号として使われます。
シグマの基本的な使い方の例を挙げます。

$\displaystyle \sum_{ k = 1 }^{ n } a_k = a_1 + a_2 + a_3 + ・・・ + a_n$

これをみてわかるように、$\displaystyle \sum_{ k = 1 }^{ n } a_k$は$a_k$のkに1,2,3,・・・,nを代入したものの和になります。

$\displaystyle \sum$の下端は右端の代数の開始数になり、ダミー変数といいます。
上端は項数を意味します。

文字だけではわかりにくいので、例を挙げます。

$\displaystyle \sum_{ k = 1 }^{ 3 } 2k = 2 × 1 + 2 × 2 + 2 × 3 = 12$

式2kにおいて、kが1から始まり項数が3の式の和を意味しています。

シグマの性質による公式をまとめます。

$$①\displaystyle \sum_{ k = 1 }^{ n } (a_k + b_k) = \displaystyle \sum_{ k = 1 }^{ n } a_k + \displaystyle \sum_{ k = 1 }^{ n } b_k$$

$$②\displaystyle \sum_{ k = 1 }^{ n } ca_k = c\displaystyle \sum_{ k = 1 }^{ n } a_k$$

$$③\displaystyle \sum_{ k = 1 }^{ n } (ca_k + db_k) = c\displaystyle \sum_{ k = 1 }^{ n } a_k + d\displaystyle \sum_{ k = 1 }^{ n } b_k $$

では、続いてこれらの性質の公式の証明です。

①の左辺を計算をすると

$(a_1 + b_1) + ・・・ + (a_n + b_n) = (a_1 + ・・・ + a_n) + (b_1 + ・・・ + b_n)$

となって、左辺 = 右辺であることがわかります。

②の左辺を計算をすると

\(c(a_1 + a_2 + ・・・ + a_n)\)

②の右辺を計算をすると

\((ca_1 + ca_2 + ・・・ + ca_n)\)
\(c(a_1 + a_2 + ・・・ + a_n)\)

左辺 = 右辺より証明されました。

③は①と②から証明できますね。

以下に、自然数、平方数、立方数の和の公式をまとめます。

$$①\displaystyle \sum_{ k = 1 }^{ n } k = 1 + 2 + 3 + ・・・ + n = {1 \over 2}n(n + 1)$$

$$②\displaystyle \sum_{ k = 1 }^{ n } k^2 = 1^2 + 2^2 + 3^2 + ・・・ + n^2 = {1 \over 6}n(n + 1)(2n + 1)$$

$$③\displaystyle \sum_{ k = 1 }^{ n } k^3 = 1^3 + 2^3 + 3^3 + ・・・ + n^3 = \{{1 \over 2}n(n + 1)\}^2$$

求める数列の和は、
1 + 2 + 3 ・・・ nの和なので、初項1、項数n、公差1の等差数列の和になるので、等差数列の和の公式より

$\displaystyle \sum_{ k = 1 }^{ n } k = {1 \over 2}n(n + 1)$

となりますね。

シグマの平方数の和の公式は、恒等式$(k + 1)^3 - k^3 = 3k^2 + 3k + 1$
から求めることができます。(恒等式から求められると覚える)

以下のようにk = 1,2,・・・nとおいて辺々を加えていきます。

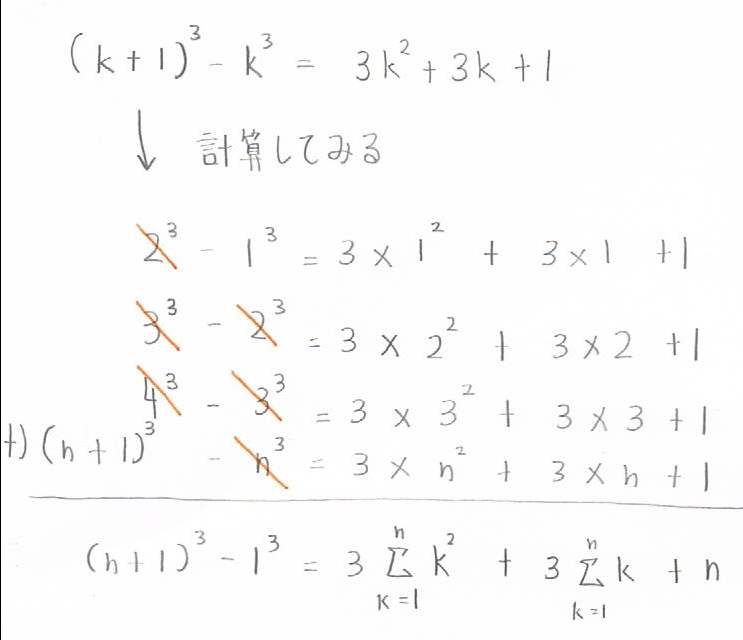
すると、$3n^2$の和が現れるので、$\displaystyle 3\sum_{ k = 1 }^{ n } k^2$を左辺に移行することで、$\displaystyle \sum_{ k = 1 }^{ n } k^2$を求めることができるので、計算をしていきます。

$\displaystyle \sum_{ k = 1 }^{ n } k^2 = {1 \over 3}\{(n + 1)^3 - 1^3 - \displaystyle 3\sum_{ k = 1 }^{ n } k - n\}$

①の公式を適応して、

$ \displaystyle = {1 \over 3} \{(n + 1)^3 - 1 - {3 \over 2}n(n + 1) - n\}$

よって$\displaystyle \sum_{ k = 1 }^{ n } k^2 = {1 \over 6}n(n + 1)(2n + 1)$

初版:2018/8/20

Tweet