複素数平面上で四角形が円に内接するための条件
複素数平面上で異なる4点A(α),B(β),C(γ),D(δ)のうち、
どの3点も一直線上にないとき、4点A,B,C,Dが一つの円周上にあるための条件は
$$\displaystyle \frac{β - γ}{α - γ} \div \frac{β - δ}{α - δ}が実数$$
1.4点A,B,C,Dがこの順に一つの円周上にあるとき
下図元にを考えます。
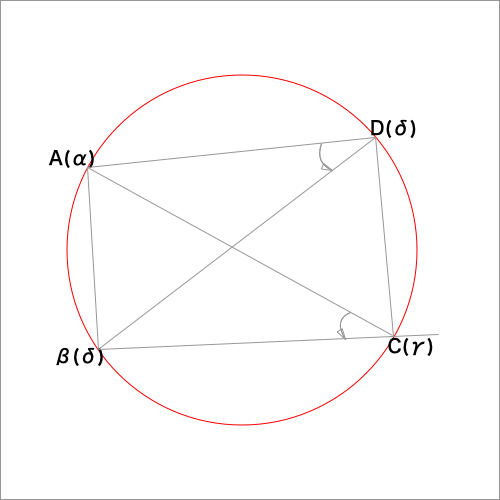
円周角の定理より
$\displaystyle arg \frac{β - γ}{α - γ} = arg \frac{β - δ}{α - δ}$
つまり、
$\displaystyle arg \frac{β - γ}{α - γ} - arg \frac{β - δ}{α - δ} = 0$
$\displaystyle arg(\frac{β - γ}{α - γ} \div \frac{β - δ}{α - δ}) = 0$
よって、
$\displaystyle \frac{β - γ}{α - γ} \div \frac{β - δ}{α - δ}$は正の実数となる
2.4点A,B,D,Cがこの順に円周上にあるとき
1.と同様に下図を考え導くことができます。
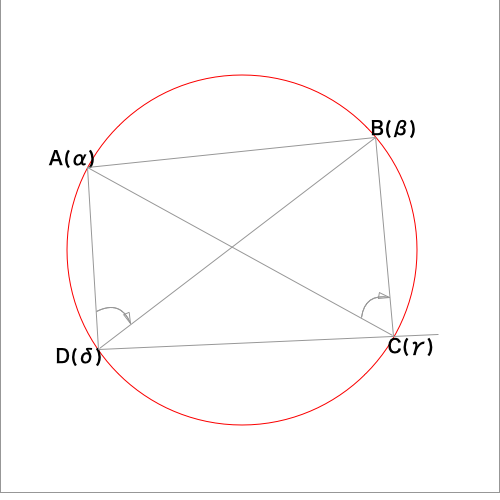
3.4点A,C,B,Dが4点A,D,B,Cがこの順に円周上にあるとき
下図を元に2つのケースを考えます。
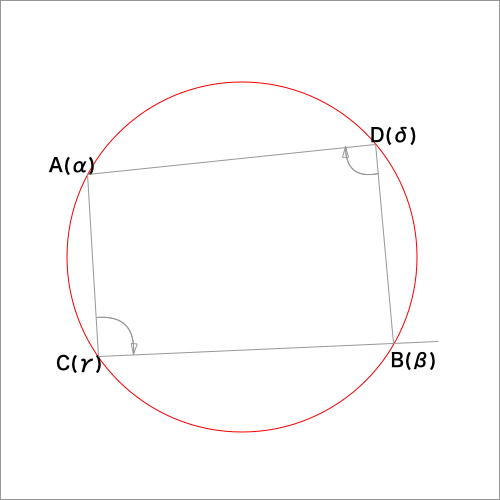
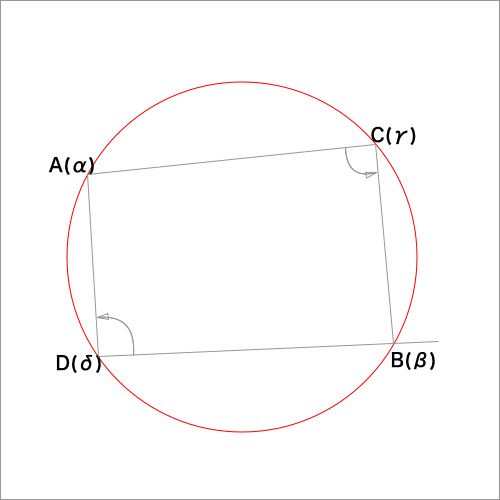
円に内接する四角形の対角の和はπであるから、
$\angle ACB + \angle BDA = π$
よって、
$\displaystyle arg \frac{β - γ}{α - γ} + arg \frac{α - δ}{β - δ} = \pm π$
$\displaystyle arg( \frac{β - γ}{α - γ} \times \frac{α - δ}{β - δ}) = \pm π$
よって、
$\displaystyle arg( \frac{β - γ}{α - γ} \div \frac{β - δ}{α - δ} )= \pm π$
以上より、
$\displaystyle \frac{β - γ}{α - γ} \div \frac{β - δ}{α - δ}$は負の実数になる。
1. ~ 3.より、
4点A,B,C,Dが一つの円周上にある $\displaystyle \Rightarrow \frac{β - γ}{α - γ} \div \frac{β - δ}{α - δ}$が実数
が言えます。
初版:2022/1/27