ドモアブルの定理とその証明について

$0$でない複素数$z$を
$z = a + bi$とすると、

$$\displaystyle (cosθ + isinθ)^n = cosnθ + isinnθ$$

が成り立ちます。

これをドモアブルの定理といいます。

先に定義した複素数$z$に対して、$z = cosθ + isinθ$をかけると、複素数の乗法の定理により、下図のように絶対値は変わらずに、
偏角$θ$だけが増えます。

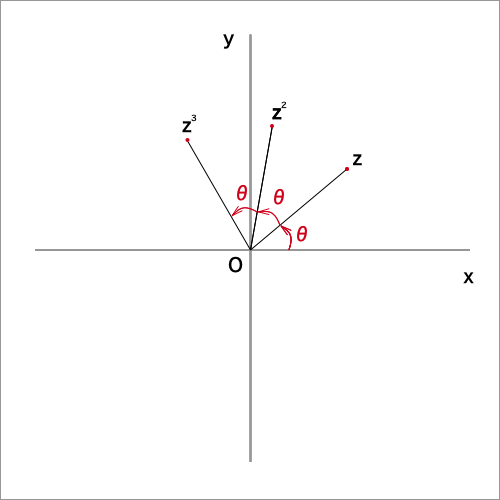
このことを用いて、$z$の累乗を考えると、

$\displaystyle (cosθ + isinθ)^2 = cos2θ + isin2θ$

$\displaystyle (cosθ + isinθ)^3 = cos3θ + isin3θ$

となり、一般の自然数$n$について、ドモアブルが成り立ちます。

$0$でない$z$に対して、$z^0 = 1$

ドモアブルより。

$cos0θ + isin0θ = 1$

$n = 0$の時も成り立ちます。

$\displaystyle z^{-n} = \frac{1}{z^n}$と定めると

$\displaystyle (cosθ + isinθ)^{-n} = \frac{1}{(cosθ + isinθ)^n}$

$\displaystyle (cosθ + isinθ)^{-n} = \frac{1}{(cosnθ + isinnθ)}$

$\displaystyle (cosθ + isinθ)^{-n} = cos(-nθ) + isin(-nθ)$

以上より、ドモアブルの定理が成立することが確認できます。

初版:2022/1/24

Tweet