複素数の除法と図形的な意味

複素数の除法について、考えます。
まず、複素数を以下のようにおきます。

$z_1 = r_1(cosθ_1 + isinθ_1)$
$z_2 = r_2(cosθ_2 + isinθ_2),(r_1 > 0,r_2 > 0)$

$\displaystyle \frac{z_1}{z_2} = \frac{r_1}{r_2}\{cos(θ_1 - θ_2) + isin(θ_1 - θ_2)\}$ - ①

また、

$\displaystyle |\frac{z_1}{z_2}| = \frac{|z_1|}{|z_2|}$

$\displaystyle arg \frac{z_1}{z_2} = argz_1 - argz_2$

極形式を当てはめます。

$\displaystyle \frac{z_1}{z_2} = z_1 \cdot \frac{1}{z_2}$でまず、
$\displaystyle \frac{1}{z_2}$を考えます。

$\displaystyle \frac{1}{z_2} = \frac{1}{r_2(cosθ_2 + isinθ_2)}$

$\displaystyle \frac{1}{z_2} = \frac{cosθ_2 - isinθ_2}{r_2(cosθ_2 + isinθ_2)(cosθ_2 - isinθ_2)}$

$\displaystyle \frac{1}{z_2} = \frac{cosθ_2 - isinθ_2}{r_2(cos^2θ_2 + isin^2θ_2)}$

$cos^2θ + sin^2θ = 1$と
$cos(-θ) = cosθ,sin(-θ) = -sinθ$より

$\displaystyle \frac{1}{z_2} = \frac{1}{r_2} \cdot \{cos(-θ_2) + isin(-θ_2)\}$

ここで、乗法の公式を利用すると、公式が求められます。

$\displaystyle \frac{z_1}{z_2} = \frac{r_1}{r_2}\{cos(θ_1 - θ_2) + isin(θ_1 - θ_2)\}$

$\displaystyle z_4 = \frac{r_1}{r_2}$とおくと

図形的に長さを考えて、$|z| = r$だから

$\displaystyle |z_4| = \frac{r_1}{r_2}$

argの定義より

$argz_4 = θ_1 - θ_2$

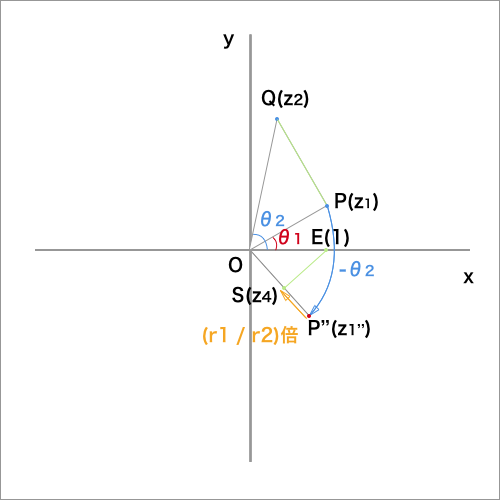
つまり下図のように、点$S(z_4)$は、点$P(z_1)$を原点Oを中心として、
角$-θ_2$だけ回転した点$P''(z_1'')$を$\dfrac{1}{r_2}$倍した点だということがわかります。

また下図のように、点E(1,0)とすると、△OPQと△OSEについて、
$\displaystyle OP : OS = r_1 : \frac{r_1}{r_2} = r_2 : 1$,
$OQ : OE = r_2 : 1,\angle POQ = \angle SOE$,

よって、
△OPQ ∽ △OSE

初版:2022/1/20

Tweet