複素数の乗法と図形的な意味

複素数の乗法について、考えます。
まず、複素数を以下のようにおきます。

$z_1 = r_1(cosθ_1 + isinθ_1)$
$z_2 = r_2(cosθ_2 + isinθ_2),(r_1 > 0,r_2 > 0)$

$z_1z_2 = r_1r_2\{cos(θ_1 + θ_2) + isin(θ_1 + θ_2)\}$ - ①

また、

$|z_1z_2| = |z_1||z_2|$

$argz_1z_2 = argz_1 + argz_2$

極形式を当てはめます。

$z_1z_2 = r_1(cosθ_1 + isinθ_1) \cdot r_2(cosθ_2 + isinθ_2)$

展開します

$z_1z_2 = r_1r_2\{(cosθ_1cosθ_2 - sinθ_1sinθ_2) + i(cosθ_1sinθ_2 + sinθ_1cosθ_2)\}$

ここで、加法定理を使うことで、求めることができます。

$z_1z_2 = r_1r_2\{cos(θ_1 + θ_2) + isin(θ_1 + θ_2)\}$

$z_3 = z_1z_2$とします。

図形的意味を考えて、$|z| = r$だから

$|z_3| = r_1r_2$

argの定義より

$argz_3 = θ_1 + θ_2$

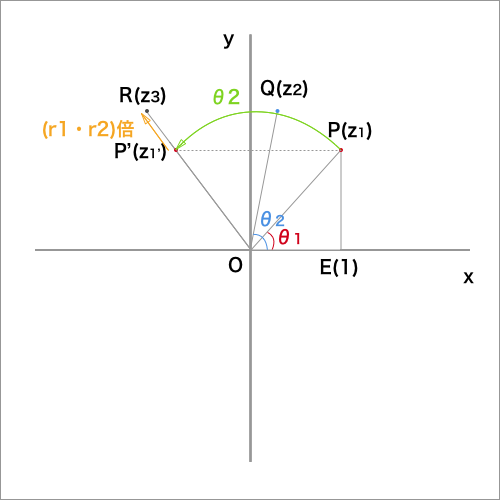
つまり下図のように、点$R(z_3)$は、点$P(z_1)$を原点Oを中心として、
角$θ_2$だけ回転した点$P'(z_1')$を$r_2$倍した点だということがわかります。

また下図のように、点E(1,0)とすると、△OEPと△OQRについて、
$OE : OQ = 1 : r_2$,$OP : OR = r_1 : r_1r_2 = 1 : r_2$,
$\angle EOP = \angle QOR$から
△OEP ∽ △OQR

初版:2022/1/19

Tweet