楕円の方程式と標準形について

下図のように平面上で、異なる2定点$F,F'$からの距離の和が一定である点$P$の軌跡を楕円という。

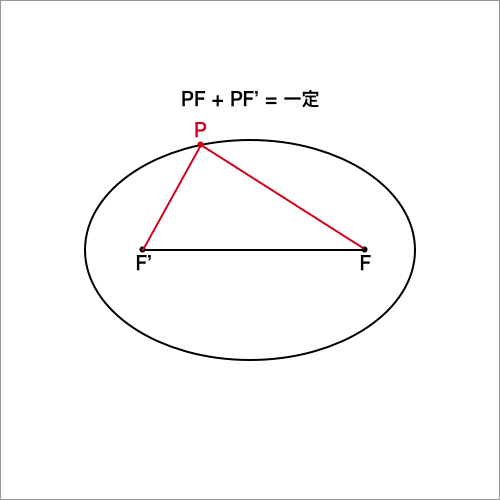
また、定点$F,F'$を楕円の焦点といい、
$PF + PF' > FF'$とする

下図のように2点$F(c,0)$,$F'(-c,0)[c > 0]$を焦点とし、
2点からの距離の和が$2a$(＊)である楕円の方程式は、

＊2焦点からの距離の和が直軸の長さである点Pの軌跡を楕円と定義します。

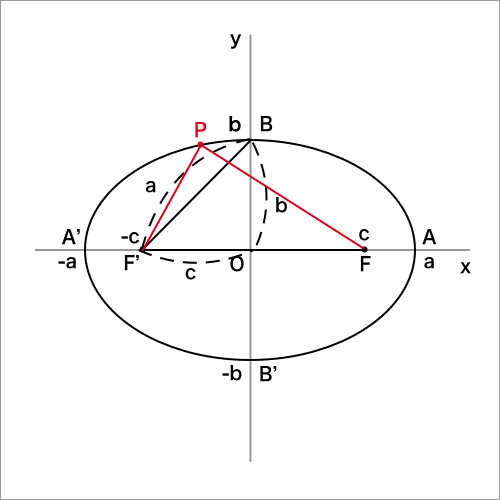
まず条件より、$PF + PF' > FF'$より
$2a > 2c$(2点からの距離の和を$2a$としている)ので、

$a > c > 0$

楕円上の点を$P(x,y)$とすると、$PF + PF' = 2a$より

$\displaystyle \sqrt{(x - c)^2 + y^2} + \sqrt{(x + c)^2 + y^2} = 2a$

$\displaystyle \sqrt{(x - c)^2 + y^2} = 2a - \sqrt{(x + c)^2 + y^2}$

両辺を2乗して整理します。

$\displaystyle x^2 -2cx + c^2 + y^2 = 4a^2 -4a\sqrt{(x + c)^2 + y^2} + x^2 +2cx + c^2 + y^2$

$\displaystyle 4a\sqrt{(x + c)^2 + y^2} = 4a^2 + 4cx$

$\displaystyle a \sqrt{(x + c)^2 + y^2} = a^2 + cx$

再び両辺を2乗して整理すると

$\displaystyle a^2(x^2 + 2cx + c^2 + y^2) = a^4 + 2a^2cx + c^2x^2$

$\displaystyle (a^2 - c^2)x^2 + a^2y^2 = a^2(a^2 - c^2)$ - ①

$a > c$だから、
$\sqrt{a^2 - c^2} = b$とおくと、
$a > b > 0$で①より

$\displaystyle b^2x^2 + a^2y^2 = a^2b^2$

両辺を$a^2b^2(\ne 0 (a > b > 0$より$))$で割ると

$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

この式を楕円の方程式の標準形といいます。

初版:2022/1/29
更新:2022/8/13(途中式を追加)

Tweet