楕円の性質と用語について

楕円の性質と用語についてまとめます。

楕円の方程式についてまとめたページにて、方程式
$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$
を導く際に、$\displaystyle \sqrt{a^2 - c^2} = b$とおいたので、
$c = \sqrt{a^2 - b^2}$になります。

よって、まとめたページで文字を置いたように、下図の楕円の焦点の座標は、

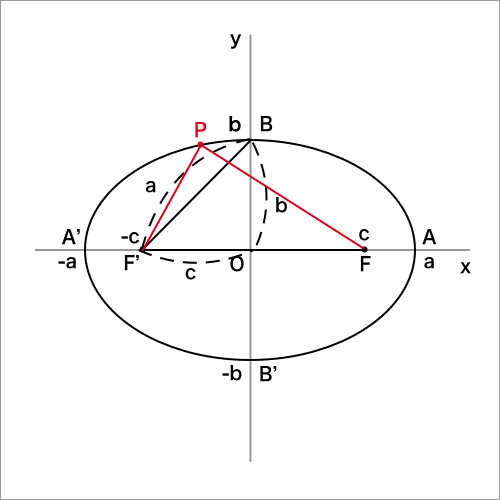
$\displaystyle F(\sqrt{a^2 - b^2,0},F'(- \sqrt{a^2 - b^2},0)$となります。

上図のように、楕円がx軸と交わる点は、A(a,0),A'(-a,0),
y軸と交わる点は、B(0,b),B'(0,-b)

この4点を楕円の頂点といいます。

上図より、a > bであるから、AA' > BB'。
長い方の線分AA'を長軸,短い方の線分BB'を短軸といい、
長軸と短軸の交点を楕円の中心といます。

ここで、いままでのことを考慮して、標準形楕円の性質をまとめます。
前提として、a > b > 0とします。

1.中心は原点、長軸の長さは2a、短軸の長さは2b

2.焦点は、2点あり,($\sqrt{a^2 - b^2},0),(- \sqrt{a^2 - b^2},0)$

3.楕円はx軸,y軸,原点に対して対象

4.楕円上の点から2つの焦点までの距離の和は2a

初版:2022/1/31

Tweet