極座標と直交座標について

極座標と直交座標についてまとめます。

平面上の点の位置を原点$O$で直行する座標軸、
$x$軸,$y$軸の組$(x,y)$のように表す座標のことを直交座標（通常使っているもの）といいます。

下図のように平面上に点$O$と半直線$OX$を定めると、この平面上の任意の点$P$の位置は、$OP$の長さ$r$と
$OX$からの半直線$OP$ヘ測った角$θ$で決まります。

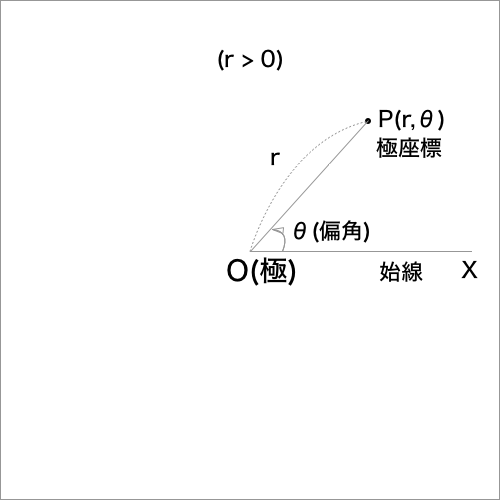
このとき、2つの数の組$(r,θ)$を点$P$の極座標といい、
定点$O$を極、半直線$OX$を始線、角$θ$を偏角といいます。

座標平面において、原点$O$を極、$x$軸の正の部分を始線とします。

このとき、同一の点$P$の極座標$(r,θ)$と直交座標$(x,y)$には、
次の関係があります。

$x = rcosθ,y = rsinθ$

$r = \sqrt{x^2 + y^2}$

$(r \ne 0)$のとき、
$\displaystyle cosθ = \frac{x}{r},sinθ = \frac{y}{r}$

これらは、三角関数を考えれば明白ですね。

初版:2022/2/6

Tweet