等加速度の公式

速さをv
距離をx
時間をt
加速度をa
初速度を$v_0$とします

$$\displaystyle x = \frac{1}{2}at^2 + v_0t$$

$$\displaystyle v = v_0 + at$$

速度の公式は
初速度に加速度を足したものという元の定義を考えれば十分だと思います。

距離の公式について説明したいと思います。
下図をご覧ください

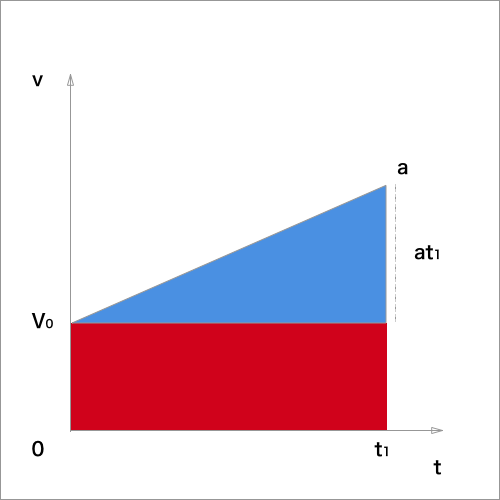
初速度を$v_0$加速度をaとします。

移動距離は速度と時間をかけると求められるので、
求める距離は、図の三角形と四角形を合わせたものになります。

四角形の面積は、$t_1 \times v_0$

次に、三角形の面積を求めるために、高さを求めます。

三角形をなす直線の傾きが加速度になっているので、
高さは、直線の方程式を考えて、$y = at_1$より、 $at_1$となります。

よって、面積は
$\displaystyle \frac{1}{2} \times at_1 \times t_1 = \frac{1}{2} at_1^2$

移動距離は2つの面積を足したものなので、

$\displaystyle \frac{1}{2}at_1^2 + v_0t_1$

と求めることができます。

初版:2022/7/1
更新:2022/10/25(速度の公式と距離の公式を分けて見やすく修正)

Tweet