等速円運動と角速度などの定義

円運動において、単位時間あたりに回転する角度を角速度ω[rad/s]という。

単振動において、1回の振動を2πとして、
単位時間における振動数を角振動数ω[rad/s](角速度と同じ記号を用いる)という。

繰り返しの運動においての一回分にかかる時間を周期という。

円運動だと一回転するまでにかかる時間というになります。

$$v = rω$$

周期を$T$、角振動数を$ω$とすると、

$$\displaystyle T = \frac{2πr}{v} = \frac{2π}{ω}$$

等速円運動の加速度を$a$、半径を$r$とすると、等速円運動の加速度は以下のように求められます。

$$\displaystyle a = rω^2 = \dfrac{v^2}{r}$$

まず、速さの定義ですが、$\dfrac{距離}{時間}$になりますね。

円運動の速さを求めるので、距離は円弧になり、$θ$回転したとすると、円弧は$rθ$と表せます。

$θ$回るのにかかった時間を$t$とすると、速度は、

$v = \dfrac{rθ}{t} - ①$

ここで、$ω$の定義は$ω = \dfrac{θ}{t}$なので、①に代入すると

$v = rω$

もう一つ簡単な証明方法があります。

円運動の周期を$T$とします。

速さ$v$とすると、円周は

$vT = 2πr - ①$

周期に角速度をかけると円を一周した時の角度つまり$2π$になるので、

$ωT = 2π - ②$

②を①に代入して

$vT = ωTr$
$v = rω$

証明するのは大変ですが、道のりは簡単なので、頭の中で公式を導けるようにしとおいた方がいいです。

加速度の定義が、

$a = \dfrac{\Delta v}{\Delta t}$

なので、$\Delta v$と$\Delta t$を求めれば、加速度が求められることになります。

まず、微小時間の回転角$ω \Delta t$を求めます。

1秒あたりの回転角がωなので、これに微小時間$\Delta t$をかければ、微小時間の回転角が求められます。

$ω \Delta t = \dfrac{v \Delta t}{r}(v = rω$より$ω = \dfrac{v}{r})$

ここで、回転角が$ω \Delta t$時の速度を考えます。
$ω \Delta t$時の速度なので、求める速度はもちろん$\Delta v$になります。

円運動している時の速度は、下図のように常に接線方向のベクトルとなります。
定義(後引く前が変位になる)により、微小角回転後と微小角回転前の速度ベクトルの差が、微小回転時の速度となります。

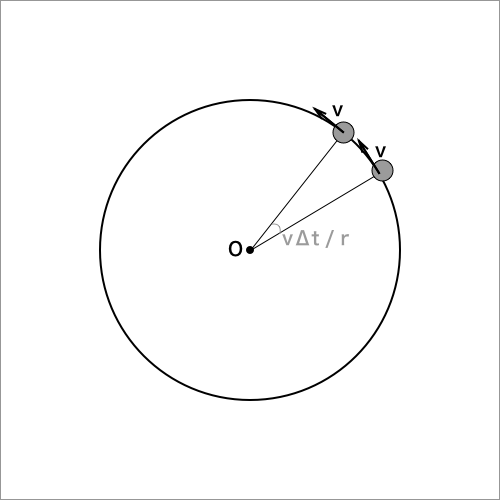
このとき、下図のように微小回転前の速度ベクトルと微小回転後速度のベクトルの始点を合わせると、
その孤の長さが速度の差つまり微小時間の速度となるので、円弧を求める公式

孤の長さ = 半径 $\times$ 中心角より

$\Delta v = v \times \dfrac{v \Delta t}{r} = \dfrac{v^2 \Delta t}{r}$

微小速度が求まったので、加速度の定義式に代入します。

$\displaystyle a = \frac{\Delta v}{\Delta t} = \frac{v^2}{r}[m / s^2]$

この式に、$v = rω$を代入すると、もう一つの式が求められます。

$\displaystyle a = rω^2$

初版:2022/7/22

更新:2022/10/10(速度の公式の証明追加)
2022/10/17(加速度の公式の証明追加)
2022/12/27(わかりやすいように図を追加した)
2023/9/28(速度の証明を追加)

Tweet