単振動について

下図のように半径Aの円の周りを質量mの物体Qが回っているとします。
ここで、Qに向けて真横から平行に光を当ててできた影を正射影と呼びます。

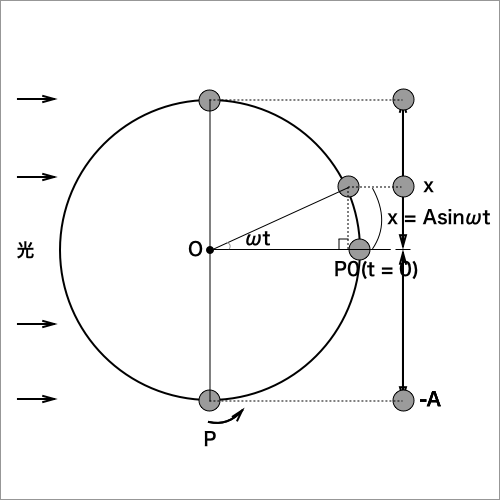
Qが円の周りを回る時、Qの正射影は原点Oを中心に往復運動するのがわかります。
このような運動を単振動と言います。

物体Pがある点から一往復するのにかかる時間を周期、単位時間に往復する回数を振動数といいます。

単振動の振幅は正射影が円の直径間で動き、中心は円と等しいので、円の半径であるAとなります。

周期は、円運動と同じで、$ \dfrac{2π}{ω}$

振動数は単位時間あたりに正射影が往復する回数なので、$\dfrac{ω}{2π}$

正射影が運動する軸をxとすると、Qの単振動の位置座標(変位)は、Qの円運動の変位のx成分なので、
下図のように、三角関数を使って、

$$x = Asinωt$$

単振動の速度をどうやって求めたらいいか、下図で確認します。

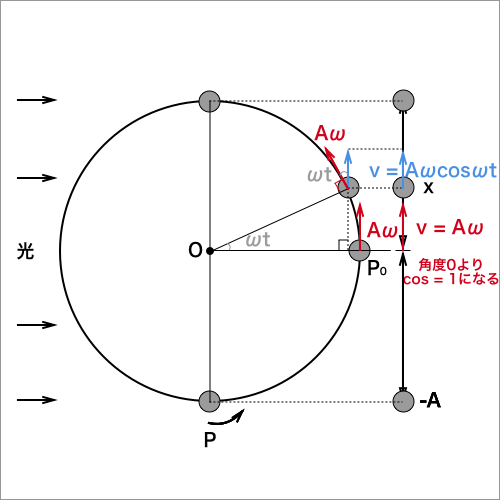
まず、等速円運動の速度はAwになりますね(等速円運動参照)。

ここで、円運動の速度Awの正射影を考えると、青の矢印の量を求めればいいことになるのがわかるので、
速度とx軸にできる直角三角形に三角関数を適応すると

$$v = Aωcosωt$$

また、単振動の最高速度は、cosθ = 1になる地点つまり、原点で最高速度Awとなります。

まず、等速円運動の加速度は$Aω^2$(別記事に解説を書いているので参照してください)になります。

速度と同じく円運動の加速度の正射影を考えます。

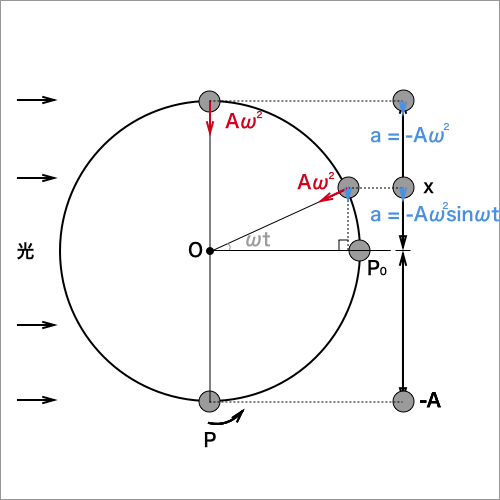
等速円運動の加速度は円の中心に向かって$Aω^2$の速度で動くので、その正射影は青色の矢印の力になります。

ここでできる直角三角形に三角関数を使うと、単振動の加速度は速度と逆向きであることに注意して

$$a = -Aω^2sinωt - ①$$

単振動はsinを使って表されるので、加速度の正射影の変異が90度を使って表される時、
つまり単振動の振幅位置で加速度が最大になります。

正射影の変異は$Asinwt$で求められるので、変位を$x$とすると

$$a = -ω^2x$$

初版:2022/9/28
改訂:2022/11/28(等速円運動の加速度へのリンクを追加)

Tweet